Корреляционный анализ Спирмена
Оглавление статьи
Описание метода ранговой корреляции Спирмена

Такие ряды могут представляться:
- парой признаков, определяемых в одной и той же группе исследуемых объектов;
- парой индивидуальных соподчиненных признаков, определяемых у 2 исследуемых объектов по одинаковому набору признаков;
- парой групповых соподчиненных признаков;
- индивидуальной и групповой соподчиненностью признаков.
Метод предполагает проведение ранжирования показателей в отдельности для каждого из признаков.
Наименьшее значение имеет наименьший ранг.
Этот метод относится к непараметрическому статистическому методу, предназначенному для установления существования связи изучаемых явлений:
- определение фактической степени параллелизма между двумя рядами количественных данных;
- оценка тесноты выявленной связи, выражаемой количественно.
Корреляционный анализ
Статистический метод, предназначенный для выявления существования зависимости между 2 и более случайными величинами (переменными), а также ее силы, получил название корреляционного анализа.
Получил свое название от correlatio (лат.) – соотношение.
При его использовании возможны варианты развития событий:
- наличие корреляции (положительная либо отрицательная);
- отсутствие корреляции (нулевая).
В качестве инструментов используются различные меры связи (коэффициенты).
На их выбор оказывает влияние:
- способ измерения случайных чисел;
- характер связи между случайными числами.
Корреляционная связь характеризуется такими признаками:
- сила связи (при коэффициенте корреляции от ±0,7 до ±1 – сильная; от ±0,3 до ±0,699 – средняя; от 0 до ±0,299 – слабая);
- направление связи (прямая или обратная).
Цели корреляционного анализа
Корреляционный анализ не позволяет установить причинную зависимость между исследуемыми переменными.
Он проводится с целью:
- установления зависимости между переменными;
- получения определенной информации о переменной на основе другой переменной;
- определения тесноты (связи) этой зависимости;
- определение направления установленной связи.
Методы корреляционного анализа

- метода квадратов или Пирсона;
- рангового метода или Спирмена.
Метод Пирсона применим для расчетов требующих точного определения силы, существующей между переменными. Изучаемые с его помощью признаки должны выражаться только количественно.
Для применения метода Спирмена или ранговой корреляции нет жестких требований в выражении признаков – оно может быть, как количественным, так и атрибутивным. Благодаря этому методу получается информация не о точном установлении силы связи, а имеющая ориентировочный характер.
В рядах переменных могут содержаться открытые варианты. Например, когда стаж работы выражается такими значениями, как до 1 года, более 5 лет и т.д.
Коэффициент корреляции
Статистическая величина характеризующая характер изменения двух переменных получила название коэффициента корреляции либо парного коэффициента корреляции. В количественном выражении он колеблется в пределах от -1 до +1.
Наиболее распространены коэффициенты:
- Пирсона – применим для переменных принадлежащих к интервально шкале;
- Спирмена – для переменных порядковой шкалы.
Ограничения использования коэффициента корреляции
Получение недостоверных данных при расчете коэффициента корреляции возможно в тех случаях, когда:
- в распоряжении имеется достаточное количество значений переменной (25-100 пар наблюдений);
- между изучаемыми переменными установлено, например, квадратичное соотношение, а не линейное;
- в каждом случае данные содержат больше одного наблюдения;
- наличие аномальных значений (выбросов) переменных;
- исследуемые данные состоят из четко выделяемых подгрупп наблюдений;
- наличие корреляционной связи не позволяет установить какая из переменных может рассматриваться в качестве причины, а какая – в качестве следствия.
Проверка значимости корреляции
Для оценки статистических величин используется понятие их значимости или же достоверности, характеризующей вероятность случайного возникновения величины либо крайних ее значений.
Его значение сравнивается с табличным, количество степенней свободы принимается как 2. При получении расчетного значения критерия больше табличного, свидетельствует о значимости коэффициента корреляции.
При проведении экономических расчетов достаточным считается доверительный уровень 0,05 (95%) либо 0,01 (99%).
Ранги Спирмена
Коэффициент ранговой корреляции Спирмена позволяет статистически установить наличие связи между явлениями. Его расчет предполагает установление для каждого признака порядкового номера – ранга. Ранг может быть возрастающим либо убывающим.
Количество признаков, подвергаемых ранжированию, может быть любым. Это достаточно трудоемкий процесс, ограничивающий их количество. Затруднения начинаются при достижении 20 признаков.
Для расчета коэффициента Спирмена пользуются формулой:
в которой:
n – отображает количество ранжируемых признаков;
d – не что иное как разность между рангами по двум переменным;
а ∑(d2) – сумма квадратов разностей рангов.
Применение корреляционного анализа в психологии
Статистическое сопровождение психологических исследований позволяет сделать их более объективными и высоко репрезентативными. Статистическая обработка данных полученных в ходе психологических экспериментов способствует извлечению максимума полезной информации.
Наиболее широкое применение в обработке их результатов получил корреляционный анализ.
Уместным является проведение корреляционного анализа результатов, полученных при проведении исследований:
- тревожности (по тестам R. Temml, M. Dorca, V. Amen);
- семейных взаимоотношений («Анализ семейных взаимоотношений» (АСВ) опросник Э.Г. Эйдемиллера, В.В. Юстицкиса);
- уровня интернальности-экстернальности (опросник Е.Ф. Бажина, Е.А. Голынкиной и А.М. Эткинда);
- уровня эмоционального выгорания у педагогов (опросник В.В. Бойко);
- связи элементов вербального интеллекта учащихся при разно профильном обучении (методика К.М. Гуревича и др.);
- связи уровня эмпатии (методика В.В. Бойко) и удовлетворенностью браком (опросник В.В. Столина, Т.Л. Романовой, Г.П. Бутенко);
- связи между социометрическим статусом подростков (тест Jacob L. Moreno) и особенностями стиля семейного воспитания (опросник Э.Г. Эйдемиллера, В.В. Юстицкиса);
- структуры жизненных целей подростков, воспитанных в полных и неполных семьях (опросник Edward L. Deci, Richard M. Ryan Ryan).
Краткая инструкция к проведению корреляционного анализа по критерию Спирмена
Проведение корреляционного анализа с использованием метода Спирмена выполняется по следующему алгоритму:
- парные сопоставимые признаки располагаются в 2 ряда, один из которых обозначается с помощью Х, а другой У;
- значения ряда Х располагаются в порядке возрастания либо убывания;
- последовательность расположения значений ряда У определяется их соответствием значений ряда Х;
- для каждого значения в ряду Х определить ранг — присвоить порядковый номер от минимального значения к максимальному;
- для каждого из значений в ряду У также определить ранг (от минимального к максимальному);
- вычислить разницу (D) между рангами Х и У, прибегнув к формуле D=Х-У;
- полученные значения разницы возводятся в квадрат;
- выполнить суммирование квадратов разниц рангов;
- выполнить расчеты по формуле:
Пример корреляции Спирмена
Необходимо установить наличие корреляционной связи между рабочим стажем и показателем травматизма при наличии следующих данных:
| Рабочий стаж в годах | Травматизм на 100 работающих |
| до 1 года | 24 |
| 1-2 | 16 |
| 3-4 | 12 |
| 5-6 | 12 |
| 7 и более | 6 |
Наиболее подходящим методом анализа является ранговый метод, т.к. один из признаков представлен в виде открытых вариантов: рабочий стаж до 1 года и рабочий стаж 7 и более лет.
Решение задачи начинается с ранжирования данных, которые сводятся в рабочую таблицу и могут быть выполнены вручную, т.к. их объем не велик:
| Рабочий стаж | Число травм | Порядковые номера | (ранги) | Разность рангов | Квадрат разности рангов |
| d(х-у) | |||||
| до 1 года | 24 | 1 | 5 | -4 | 16 |
| 1-2 | 16 | 2 | 4 | -2 | 4 |
| 3-4 | 12 | 3 | 2,5 | +0,5 | 0,25 |
| 5-6 | 12 | 4 | 2,5 | +1,5 | 2,5 |
| 7 и более | 6 | 5 | 1 | +4 | 16 |
| Σ d2 = 38,5 |
Появление дробных рангов в колонке связано с тем, что в случае появления вариант одинаковых по величине находится среднее арифметическое значение ранга. В данном примере показатель травматизма 12 встречается дважды и ему присваиваются ранги 2 и 3, находим среднее арифметическое этих рангов (2+3)/2= 2,5 и помещаем это значение в рабочую таблицу для 2 показателей.
Выполнив подстановку полученных значений в рабочую формулу и произведя несложные расчёты получаем коэффициент Спирмена равный -0,92
Отрицательное значение коэффициента свидетельствует о наличии обратной связи между признаками и позволяет утверждать, что небольшой стаж работы сопровождается большим числом травм. Причем, сила связи этих показателей достаточно большая.
Следующим этапом расчётов является определение достоверности полученного коэффициента:
• рассчитывается его ошибка и критерий Стьюдента

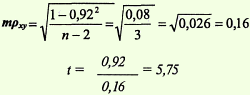
Для нахождения уровня значимости обращаемся к таблице Критические значения коэффициента корреляции рангов Спирмена, в которой приведены критические значения для коэффициентов ранговой корреляции.